Diving Knowledge Workbook: Displacement
For this next installment of the Diving Knowledge Workbook Blog series, we are going to skip ahead slightly to Objective 1.5 and discuss one of the more difficult aspects of the physics section for many candidates: lifting objects and calculating buoyancy.
Let’s take a look at the question before we dive into the details!
As I said this is from objective 1.5:
Approximately how much water must be displaced to bring a 500 kilogram object to the surface if the object displaces 300 liters? The object lies in 40 meters of seawater.
a. Slightly more than 300 liters
b. Slightly more than 185 liters
c. Slightly more than 29 liters
d. The answer cannot be determined from the data provided

All of these buoyancy questions that we must calculate during our exams all stem from the same theory, Archimedes Principle!
Archimedes Principal states that – “an object wholly or partially immersed in a fluid is buoyed up by a force equal to the weight of the fluid that it displaces”.
Archimedes was a famous scientist who went down in history for running naked through the streets of Syracuse screaming “Eureka!” after having a bath and realizing his theory of displacement….true story, look it up!
Anyways, naked scientists aside, to oversimplify his theory, it essentially says that any object that is pushing water away, the weight of that water is pushing right back trying to bring the object to the surface.
Now where buoyancy comes in to play is the weight of the displacement in comparison to the weight of the object. If the displacement weighs more than the object, it will be positively buoyant. If the displacement weighs less than the object, it will be negatively buoyant; and if the displacement weighs the same as the object, it will be neutrally buoyant. Now when we are discussing these questions, neutral buoyancy is what we are aiming for.
So simply speaking to answer the above question, all we need to do is figure out the difference between the displacement of the object and the weight of the object and compensate for the difference by displacing additional water, usually with a lift bag.
Sounds simple enough but liters and kilograms are not compatible, so we must convert one to match the other and this is where most confusion arises. However, keep in mind that it is not as daunting as it sounds because we have some constants available to us which will also be printed in the cover of your final exams! The constant we want to focus on here is 1 liter of salt water weighs 1.03 kilograms.
Alright so let’s get back to the question. A good approach to these types of questions is to cut out the information that you don’t need and focus on what we do need. For instance, in any given question such as this, we need 3 components:
- the weight of the object – kilograms
- the displacement of the object – liters
- the environment – salt or fresh water
Without all three of these, we cannot determine the answer.
Now let’s separate the information we need and forget about the rest.
- the weight of the object – 500 kilograms
- the displacement of the object – 300 liters
- the environment – salt water
In this case, 40 meters of depth does not matter, so we can forget about it as it’s likely a number that will just confuse us.
Now we need to convert everything in to something that is compatible. So either all liters or all kilograms, not one of each, as liters is a measurement of volume and kilograms is a measurement of weight. The easiest approach to this is to establish what measurement the final answer will need to be in and then convert all of our information in to this same measurement.
In our case “how much water must be displaced” which is a measurement of volume and therefore we will use liters.
So how do we convert kilograms into liters so we can find the difference between the weight and displacement? It’s actually quite simple as we have the previously mentioned constant that is 1 liter of seawater weighs 1.03 kilograms, the only thing to know is do we divide by 1.03 or multiply by 1.03?
For this I teach all of my candidates a very basic diagram
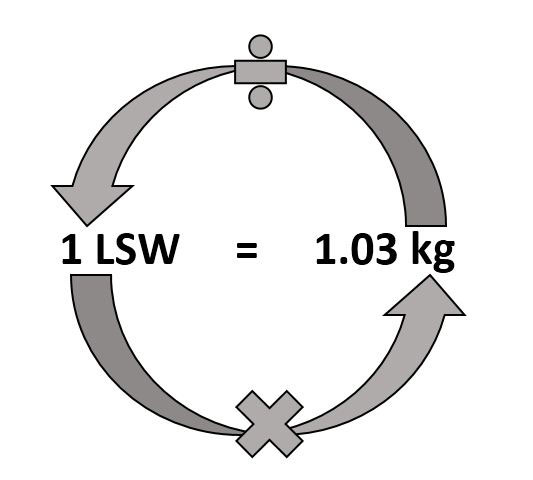
If we know that 1 liter is equal to 1.03 kilograms. To get from 1 (liter) to 1.03 (kilograms) you would have to multiply. And in the opposite to get from 1.03 (kilograms) to 1 (liter) you would have to divide.
Essentially to get from a smaller number to a larger number we need to multiply and to get from a larger number to a smaller number we would need to divide. So just by looking at the above diagram we can quickly establish whether we need to divide or multiply when converting.
So therefore we need to convert the 500kg into a measurement of liters as follows:
500kg / 1.03 = 485l
This shows us that 500kg weighs as much as 485l of seawater. Now all we need to do is find the difference by subtracting the displacement:
485L – 300L = 185l
This shows that we must displace an additional 185l of seawater to achieve a total displacement equal to the weight of the object or better known as neutral buoyancy, and you have your answer!
b. Slightly more than 185 liters
These questions and equations can take a bit of practice but at the end of the day don’t worry! Just take your time and remember the exams provide some constants for us. Hopefully this helped a bit as you are preparing for your IDC and making your way through the diving knowledge workbook. If you are still shopping around, don’t hesitate to check out our IDC program at Blue Season Bali and send us an email for details!



